Your Stable matching and analytics images are ready. Stable matching and analytics are a topic that is being searched for and liked by netizens today. You can Get the Stable matching and analytics files here. Get all free photos.
If you’re searching for stable matching and analytics images information connected with to the stable matching and analytics topic, you have come to the right site. Our site frequently provides you with suggestions for viewing the maximum quality video and image content, please kindly search and find more enlightening video content and images that fit your interests.
Stable Matching And Analytics. The matching m1 w1 and m2 w2 is stable because there are no two people of opposite sex that would prefer each other over their assigned partners. Stable Matching John P. The Marriage Model. We study stability of twosided manytoone matching in which firms preferences for workers may exhibit complementarities.
Mathematical Models For Stable Matching Problems With Ties And Incomplete Lists Sciencedirect From sciencedirect.com
A discrete choice model assumes that an observed match reveals group partners preferences over each other. The college admissions and stable marriage problems. Given the preference lists of n hospitals and n students find a stable matching if one exists. The matchingMarkets package contains R C and Java code for stable matching algorithms and the estimation of structural models that correct for the sample selection bias of observed outcomes in matching markets. Although such preferences are known to jeopardize stability in a finite market we show that a stable matching exists in a large market with a continuum of workers provided that each firms choice is convex and changes continuously as the set of available workers changes. The use of a stable matching algorithm typically requires complex and time-consuming calculations to ensure the behaviour of an OQ switch is maintained.
4 Analysis of Stable Matchings in R.
It is always possible to form stable marriages from lists of preferences See references for proof. As in any game-theoretic analysis it will be important in what follows to keep clearly in mind the rules of the game by which men and women may become married to one another as these will influence every aspect of the. The college admissions and stable marriage problems. An R package for the analysis of stable matchings. In this matching both men are matched to their first choices which is not the case for the women. It is always possible to form stable marriages from lists of preferences See references for proof.
Source: medium.com
9 1st 2nd 3rd Atlanta Xavier Yolanda Zeus Boston Yolanda Xavier Zeus Chicago Xavier Yolanda Zeus 1st 2nd 3rd Xavier Boston Atlanta Chicago. Given a set of preferences among hospitals and medical school students design a self-reinforcing admissions process. For example who works at which job which. In version of GS where men propose each man receives best valid partner. Basics of Algorithm Analysis.
Source: amazon.com
In version of GS where men propose each man receives best valid partner. Given preference profiles of n men and n women find a stable matching. The stable matching problem in its most basic form takes as input equal numbers of two types of participants n men and n women or n medical students and n internships for example and an ordering for each participant giving their preference for whom to be matched to among the participants of the other typeA stable matching always exists and the algorithmic problem solved by the Gale. By Lemma 1 and Lemma 2 the output of the Gale-Shapley algorithm is perfect matching with no instabilities. Following is GaleShapley algorithm to find a stable matching.
Source: mdpi.com
The matchingMarkets package contains R C and Java code for stable matching algorithms and the estimation of structural models that correct for the sample selection bias of observed outcomes in matching markets. 2 Matching Residents to Hospitals Goal. Basics of Algorithm Analysis. Of course this gender bias can be reversed but not eliminated by reversing the roles played by men and women in the. However the observed matching is the outcome of complex interactions and con icts of interest between the players in.
Source: sciencedirect.com
Of course this gender bias can be reversed but not eliminated by reversing the roles played by men and women in the. Stable Matching Summary Stable matching problem. X prefers y to their assigned hospital. Given a set of preferences among hospitals and medical school students design a self-reinforcing admissions process. Implements a Bayes estimator that corrects for sample selection in matching markets when the selection process is a one-sided matching game ie.
Source: link.springer.com
The matching m1 w1 and m2 w2 is stable because there are no two people of opposite sex that would prefer each other over their assigned partners. Implements a Bayes estimator that corrects for sample selection in matching markets when the selection process is a one-sided matching game ie. 2 Matching Residents to Hospitals Goal. The algorithm terminates in at most n 2 n2 n 2 iterations. Basics of Algorithm Analysis.
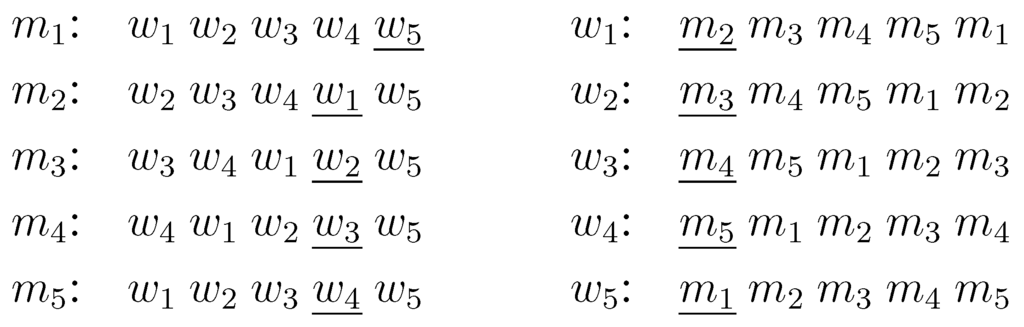Source: mdpi.com
It assigns to each man the highest-ranked woman possible under any stable marriage. Stable Matching Summary Stable matching problem. 9 1st 2nd 3rd Atlanta Xavier Yolanda Zeus Boston Yolanda Xavier Zeus Chicago Xavier Yolanda Zeus 1st 2nd 3rd Xavier Boston Atlanta Chicago. Applicant x and hospital y are unstable if. The stable matching problem in its most basic form takes as input equal numbers of two types of participants n men and n women or n medical students and n internships for example and an ordering for each participant giving their preference for whom to be matched to among the participants of the other typeA stable matching always exists and the algorithmic problem solved by the Gale.
Source: link.springer.com
An algorithm is efficient if when implemented it runs quickly on real input instances. A discrete choice model assumes that an observed match reveals group partners preferences over each other. Implements the Bayes estimator for a two-sided matching game ie. The matching m1 w1 and m2 w2 is stable because there are no two people of opposite sex that would prefer each other over their assigned partners. For example who works at which job which.
Source: link.springer.com
The Gale-Shapley algorithm always outputs a stable matching. Package matchingMarkets Heckman model. When a switch of this architecture uses a stable matching algorithm to transfer packets across the switch fabric an output queued OQ switch can be mimicked exactly with a speedup of only two. An algorithm is efficient if when implemented it runs quickly on real input instances. It assigns to each man the highest-ranked woman possible under any stable marriage.
Source: amperity.com
Analysis of Algorithms I Stable Matching Paul Beame. Matching is concerned with who transacts with whom and how. Given preference profiles of n men and n women find a stable matching. A discrete choice model assumes that an observed match reveals group partners preferences over each other. Does man-optimality come at the expense of the women.
Source: researchgate.net
4 Analysis of Stable Matchings in R. Given a set of preferences among hospitals and medical school students design a self-reinforcing admissions process. When a switch of this architecture uses a stable matching algorithm to transfer packets across the switch fabric an output queued OQ switch can be mimicked exactly with a speedup of only two. 4 Runtime Analysis The algorithm begins with n2 time to setup the needed data structures then runs the main. The Gale-Shapley algorithm always outputs a stable matching.
Source: link.springer.com
It is always possible to form stable marriages from lists of preferences See references for proof. 9 1st 2nd 3rd Atlanta Xavier Yolanda Zeus Boston Yolanda Xavier Zeus Chicago Xavier Yolanda Zeus 1st 2nd 3rd Xavier Boston Atlanta Chicago. Basics of Algorithm Analysis. An algorithm is efficient if when implemented it runs quickly on real input instances. The stable matching problem in its most basic form takes as input equal numbers of two types of participants n men and n women or n medical students and n internships for example and an ordering for each participant giving their preference for whom to be matched to among the participants of the other typeA stable matching always exists and the algorithmic problem solved by the Gale.
Source: link.springer.com
The stable matching problem in its most basic form takes as input equal numbers of two types of participants n men and n women or n medical students and n internships for example and an ordering for each participant giving their preference for whom to be matched to among the participants of the other typeA stable matching always exists and the algorithmic problem solved by the Gale. We study stability of twosided manytoone matching in which firms preferences for workers may exhibit complementarities. 2 Matching Residents to Hospitals Goal. In this matching both men are matched to their first choices which is not the case for the women. By Lemma 1 and Lemma 2 the output of the Gale-Shapley algorithm is perfect matching with no instabilities.
Source: sciencedirect.com
A discrete choice model assumes that an observed match reveals group partners preferences over each other. 4 Analysis of Stable Matchings in R. However the observed matching is the outcome of complex interactions and con icts of interest between the players in. Does man-optimality come at the expense of the women. One can prove that the algorithm always yields a stable matching that is man-optimal.
Source: mdpi.com
Given preference profiles of n men and n women find a stable matching. A discrete choice model assumes that an observed match reveals group partners preferences over each other. In version of GS where men propose each man receives best valid partner. Following is GaleShapley algorithm to find a stable matching. Video lesson on the stable matching problem and how it is solved by the Gale Shapley algorithmReferences1.
Source: sciencedirect.com
Package matchingMarkets Heckman model. In version of GS where men propose each man receives best valid partner. Video lesson on the stable matching problem and how it is solved by the Gale Shapley algorithmReferences1. One can prove that the algorithm always yields a stable matching that is man-optimal. Applicant x and hospital y are unstable if.
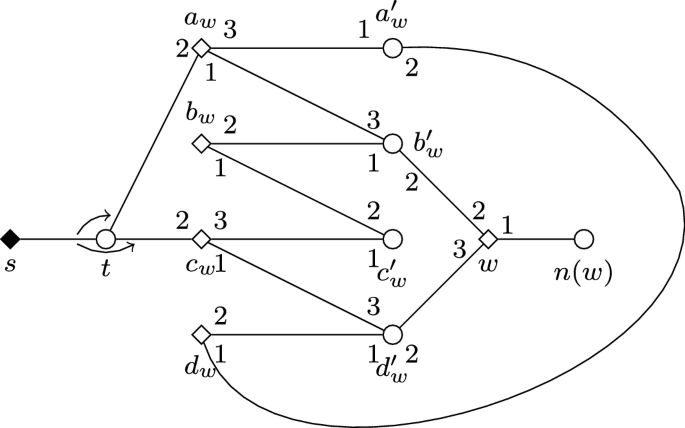Source: link.springer.com
Implements a Bayes estimator that corrects for sample selection in matching markets when the selection process is a one-sided matching game ie. In this matching both men are matched to their first choices which is not the case for the women. The stable matching problem in its most basic form takes as input equal numbers of two types of participants n men and n women or n medical students and n internships for example and an ordering for each participant giving their preference for whom to be matched to among the participants of the other typeA stable matching always exists and the algorithmic problem solved by the Gale. Implements the Bayes estimator for a two-sided matching game ie. 4 Runtime Analysis The algorithm begins with n2 time to setup the needed data structures then runs the main.
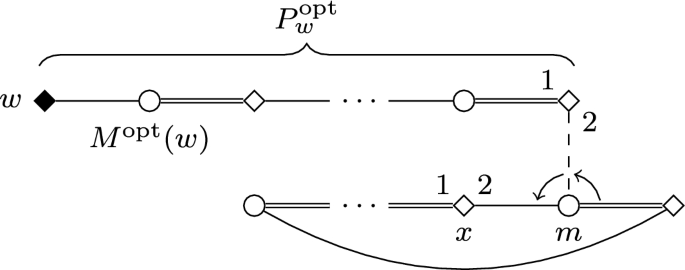Source: link.springer.com
The matching m1 w1 and m2 w2 is stable because there are no two people of opposite sex that would prefer each other over their assigned partners. The algorithm terminates in at most n 2 n2 n 2 iterations. Two-Sided Matching - September 1990. Given a set of preferences among hospitals and medical school students design a self-reinforcing admissions process. 9 1st 2nd 3rd Atlanta Xavier Yolanda Zeus Boston Yolanda Xavier Zeus Chicago Xavier Yolanda Zeus 1st 2nd 3rd Xavier Boston Atlanta Chicago.
Source: towardsdatascience.com
Implements a Bayes estimator that corrects for sample selection in matching markets when the selection process is a one-sided matching game ie. By Lemma 1 and Lemma 2 the output of the Gale-Shapley algorithm is perfect matching with no instabilities. For example who works at which job which. Matching is concerned with who transacts with whom and how. Basics of Algorithm Analysis.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title stable matching and analytics by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
